Ako ďaleko vidíte meteor?
>Príde mi email.
Väčšina z nich kladie otázky rôzneho druhu, na väčšinu z nich je dosť jednoduchá odpoveď (v skutočnosti by sa dalo na veľa odpovedať googlením, nápoveda). Niekedy však dostanem otázku, na ktorú je ťažšie odpovedať, alebo dokonca otázku, na ktorú som sám premýšľal, ale nikdy som ju nedokázal prísť na to.
Takže ma celkom zaujalo, keď som dostal otázku od Bad Readera Deana Lewisa o meteoroch. Počas meteorického roja Perseid v roku 2018 bol preč od svojej rodiny, delí ho asi 1 000 kilometrov. Ak by videl meteor, bolo by možné, aby videli ten istý zo svojho vzdialenejšieho miesta?
Krátka odpoveď je: Áno! Dlhá odpoveď je ... matematika. Super, zábavná matematika.
A keďže keď uverejníme tento článok, výročná meteorická sprcha Geminid v roku 2018 dnes večer vrcholí, myslím si, že je vhodné na to prísť.
Crash Course Astronomy: Meteory, meteoroidy a meteority, ach jaj!
Ak bola Zem dokonale plochá, potom by ste v zásade mohli vidieť meteor až na akýkoľvek okraj Zeme. Pokiaľ ste nad zemou, aj keď ste maličký, potom váš zorný uhol dosiahne každý centimeter štvorcový planéty na vašej strane, takže každý meteor bude viditeľný pre každého. V skutočnosti nie je vzduch úplne priehľadný, takže v určitej vzdialenosti sa pozeráte cez toľko bahna, že nič nevidíte.
Zem však nie je plochá. Vážne! Je to okrúhle. A atmosféra ju obklopuje ako škrupina, s výškou sa stenčuje a nakoniec ustupuje; táto výška závisí od vašej definície priestoru. Môžeme však trochu podvádzať, pretože poznáme vedu: Meteory ako tie v sprchách majú tendenciu horieť asi 100 kilometrov nad zemou. Táto výška závisí od mnohých vecí, vrátane veľkosti meteoroidy (pevné časti medziplanetárnych úlomkov, ktoré sa šíria priestorom), sú to, ako rýchlo sa pohybujú, pod akým uhlom vstupujú do atmosféry a podobne. Nazvime to však 100 km.
Meteor vám môže byť najbližšie, ak ste priamo pod ním, a potom je to 100 km priamo hore (za vašim zenitom). Ak to zhorí ďalej od zenitu, potom to musí byť ďalej od vás. Podľa rozumu je najvzdialenejší meteor, ak je teda presne na obzore.
Geometria vyzerá takto (poznámka: NIE v mierke):
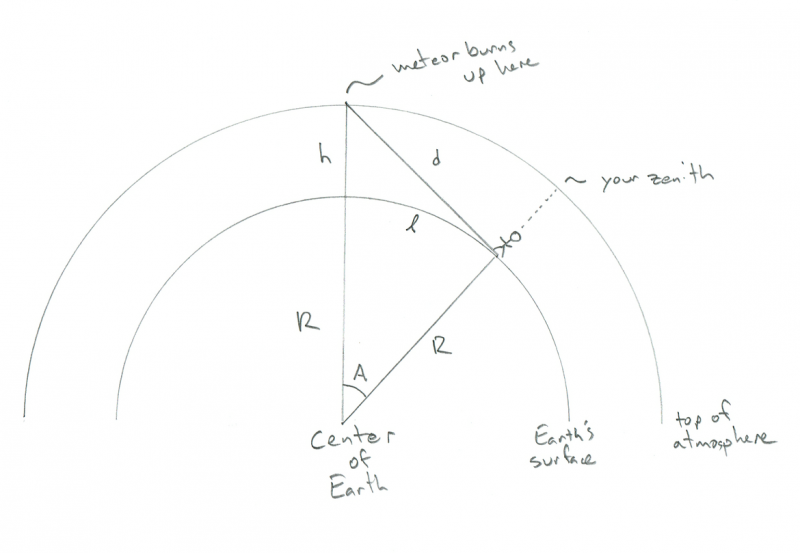
Schéma znázorňujúca geometriu pozorovateľa sledujúceho horiaci meteor. Kredit: Phil Plait
Môžete vidieť malého panáčika, ktorý stojí na povrchu zakrivenej Zeme - povedzme, že ste to vy - s (aj zakrivenou) atmosférou nad nimi. V tomto diagrame R je polomer Zeme (6 000 000 km), h je výška, v ktorej meteor horí (100 km) a d je vzdialenosť od vás k meteoru. A je uhol medzi vašou polohou na Zemi a polohou meteoru nad ním a cursive l (ako na dĺžku) je vzdialenosť, ktorú musíte prejsť, aby bol meteor priamo nad hlavou (viem, že to vyzerá ako zvláštna vec chcieť vedieť, ale vydržať so mnou). Zvláštne, môžete tu vypočítať všetko, čo potrebujete, bez toho, aby ste vedeli d, ale potom je skvelé vedieť, ako ďaleko je meteor, že?
Kľúčom k tomu všetkému je vidieť, že uhol medzi meteorom, vami a stredom Zeme je pravý uhol. Je to preto, že meteor je na obzore, ako ho vidíte (alebo, ak dávate prednosť zábavnému žargónu, na dotyčnici vo vnútornom kruhu, kde ho pretína R). Vďaka tomu je trojuholník pravým trojuholníkom a ak si pamätáte stredoškolskú matematiku, znamená to, že nájdete všetky strany a uhly!
Pamätajte si Pytagorova veta ? V pravom trojuholníku je štvorec dĺžky prepony rovný súčtu štvorcov ostatných dvoch strán.*. V našom trojuholníku je prepona R+h a ostatné strany sú R a d.
Takže
(R+h)2= d2+ R.2
alebo vynásobením ľavej strany (použite FÓLIA ):
R.2+ 2Rh + h2 = d2+ R.2
okraj recenzie svetového filmu
Vyriešte d, aby ste videli, ako ďaleko je meteor od vás. Všimnite si toho, že R2 je na oboch stranách, takže ich zrušením získate
d2= 2Rh + h2
Alebo
d = druhá odmocnina (2Rh + h2)
Poznáme všetky tie čísla! Plug-n-chug, dieťa:
d = druhá odmocnina (2 x 6 400 x 100 + 10 000) = 1 136 km
Aha! To znamená, že ak vidíte na obzore meteor, je vzdialený viac ako 1100 kilometrov! Je to dlhá cesta a technicky najďalej môžete vidieť meteor zo zeme.
Teraz nájdeme kurzívum l. Najprv musíme poznať uhol A. To vyžaduje určitú trigonometriu. Existuje veľa spúšťacie identity Môžete na to prísť, ale môj obľúbený†je, že v pravom trojuholníku je sínus uhla dĺžkou protiľahlej strany delenou dĺžkou prepony. Ak teda dostaneme tento pomer, môžeme vziať inverzný sínus (alebo arcsín), aby sme získali uhol.
hriech (A) = d / (R + h)
takže
A = bez-1(d / R + h)
Plug-n-chug znova, a dostanem A = 10 °. To je slušný kus zemského povrchu!
čas jazdy pre dievča vo vlaku
A teraz môžeme dostať kurzívnu l. Okolo Zeme je 360 ° a obvod Zeme je 2 x pi x polomer = 40 192 km, takže existuje
40 192 km / 360 ° = 112 kilometrov na stupeň
čo znamená zasa 10 ° = 1 120 kilometrov. To je dosť blízko k d, čo nie je príliš prekvapujúce. Kresby sú prehnané, ale v skutočnosti je škrupina vzduchu nad nami v porovnaní s veľkosťou Zeme malá. Ak by som nakreslil výkresy v mierke, videli by sme, že d a l sú si skutočne dosť blízke.
Dobre, tak prečo som celý horúci a obťažujem sa nájdením l? Kvôli pôvodnej otázke! Ak ste po tej matematike zabudli, je to, ako ďaleko môžu byť dvaja ľudia a stále vidia ten istý meteor?
V takom prípade by bol meteor priamo medzi nimi a na každom z ich príslušných horizontov. Geometria vyzerá takto:
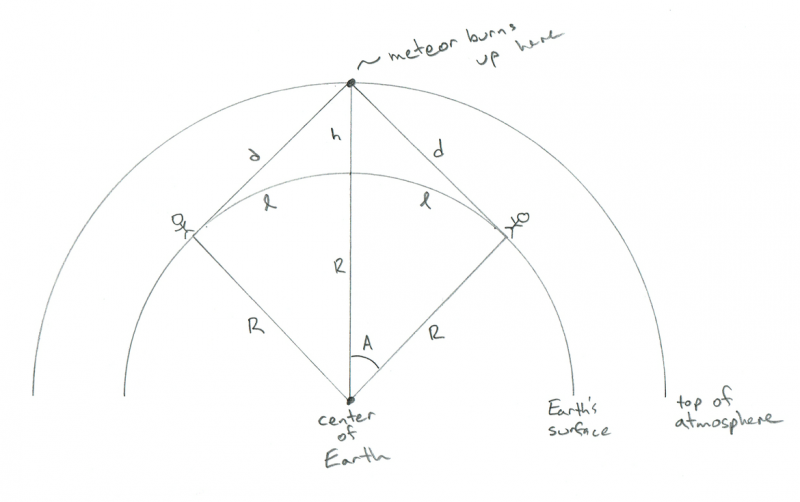
Schéma zobrazujúca geometriu dvoch pozorovateľov sledujúcich meteor, ktorý horí presne medzi nimi. Kredit: Phil Plait
AHA! Teraz vidíte, prečo chcem l! Vzdialenosť medzi týmito dvoma ľuďmi je iba 2 x l! Takže teraz máme odpoveď:
Aby dvaja ľudia videli ten istý meteor, môžu byť od seba vzdialení maximálne 2 x 1 120 = 2 240 kilometrov. Ako príklad je to veľmi blízko vzdialenosti medzi Washingtonom, DC a Denverom. Wow.
Mimochodom, pre zmenu perspektívy (doslova) to z pohľadu meteoritu znamená, že môže vidieť úsek Zeme široký 2 240 kilometrov (ako v DC na východnom údu Zeme a Denver na západnom). To je v pohode
A tým sa dostávame k skutočnej odpovedi na Deanovu otázku: Ak by bol 1 000 km od svojej rodiny, potom áno, technicky by mohli vidieť ten istý meteor. Čo s tým?
Teraz to opäť predpokladá, že vzduch je úplne čistý a to všetko, čo je v skutočnosti v podstate nemožné. Táto matematika teda predstavuje ideálnu situáciu (vrátane predstavy, že meteor je presne medzi nimi).
Buďme realistickejší. Povedzme, že meteor pre oboch pozorovateľov zhorí na oblohe vo výške 45 ° nad obzorom. Ako ďaleko by boli jeden od druhého? Opäť, za predpokladu, že je meteor presne medzi nimi, je geometria podobná tejto:
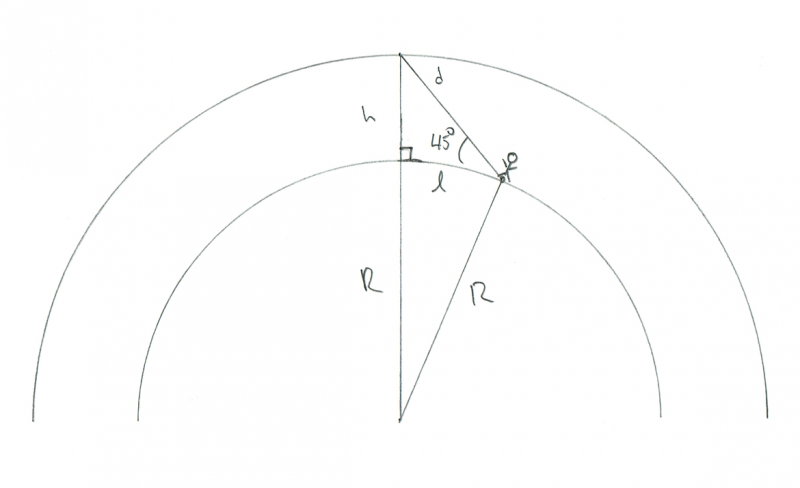
Schéma znázorňujúca geometriu pozorovateľa sledujúceho meteor horiaci 45 ° nad obzorom. Kredit: Phil Plait
Riešenie je v skutočnosti ťažšie, ale poznám ďalší trik: Ak predpokladáme, že l je malé, potom zakrivenie Zeme nebude dôležité. Napríklad, ak chcem poznať vzdialenosť medzi dvoma stromami vo svojom dvore, je mi jedno, že Zem je zakrivená. Na takú malú vzdialenosť môžem predpokladať, že je plochý. Urobme tu tento predpoklad.
V tom prípade tu máme ďalší pravouhlý trojuholník, ale tentokrát je pravým uhlom ten pod meteoritom. Dokonca som to označil v diagrame vecou s malým štvorcovým zápisom. Ak je to teda uhol 90 ° a náš uhol k meteoritu je 45 °, potom posledný uhol (od meteoru k pozorovateľovi) je tiež 45 °. To znamená, že musí ísť o rovnoramenný trojuholník, takže l a h sú rovnaké! Pretože vieme, že h je 100 km, tak aj l.
A to znamená, že vzdialenosť medzi našimi dvoma pozorovateľmi je dvojnásobná alebo 200 km.
Mimochodom, v tomto prípade je vzdialenosť k meteoru asi 141 km. Potvrdenie toho ako cvičenia nechám na čitateľa.
V zásade to znamená, že ak viete, ako vysoko je na obzore meteor, a nadmorskú výšku, v ktorej zhorel, môžete vypočítať jeho vzdialenosť (alebo ak poznáte vzdialenosť, môžete zistiť jej výšku). Tento trig je však dosť komplikovaný a myslím si, že som pre vás na dnes hodil dostatok matematiky.
Je však skvelé si myslieť, že trochu matematiky na strednej škole môže mať takú zábavnú aplikáciu. A priznávam, že je poetické a romantické vedieť, že pokiaľ nie je odlúčenie príliš ďaleko, je možné zdieľať pohľad na padajúcu hviezdu s niekým iným. Aká krásna myšlienka.
* V Čarodejník z krajiny Oz , strašiak to zle pochopil po dostal mozog.
† Z kurz Mám obľúbenú identitu trig. Čo je tvoje?













